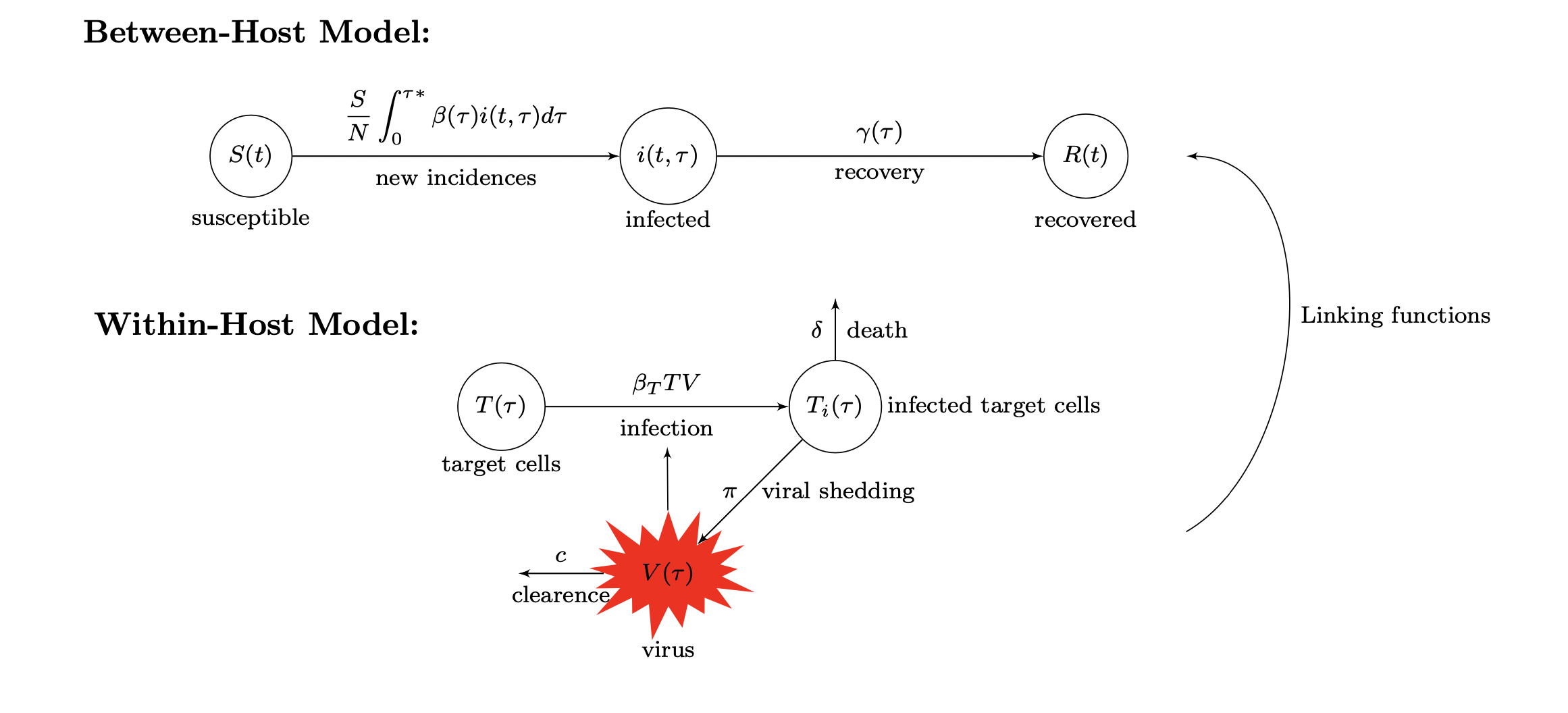
Fitting Multi-Scale Data to Multi-Scale Models
Nowadays, thanks to the advanced technology time series data of biological processes at every scale is available. So we can use parameter estimation tools to compute the parameters of the models from the time series data of the observed state. We are taking a systematic approach to this ill-posed inverse problem by first studying the well-posedness of the parameter estimation problem. That is, we first determine whether the parameters of the model can be identified from the given observed state. This is termed as structural identifiability in system biology. If you have an ODE model, you can determine whether your model is structurally identifiable by using software DAISY (Differential Algebra for Identifiability of SYstems). Unfortunately, there are no such analytical tools available for nested PDE models such as the ones we are working on. This is the topic of our current research interest. Structural identifiability analysis (if done through Differential Algebra Approach) gives you which parameters or combinations of parameters are identifiable. Furthermore, if the model is not identifiable, through this analysis you can determine what other state variables need to be observed so that you get a well-posed parameter estimation problem.
Let's say, you successfully completed the first step and obtained a structurally identifiable (ODE) model, but unfortunately this is not enough to state that the parameters you obtained through fitting is optimal parameters. Because, the structural identifiability analysis is done in a mathematician's ideal world; it assumes that there are no noise in the observed state. Clearly, in practice there are measurement errors in the data and hopefully you know the error structure. Moreover, to estimate the parameters you need to solve an optimization problem. The numerical methods to solve the optimization problem are iterative solvers, that is depending on your initial guess it may or may not find the global minimum. So, as a second step you need to determine whether the parameters can be identified in practice, and perform practical identifiability analysis.